역전파는 신경망 훈련의 본질입니다.
이전 에포크 (즉, 반복)에서 얻은 오류율 (즉, 손실)을 기반으로 신경망의 가중치를 미세 조정하는 방법입니다. 가중치를 적절하게 조정하면 오류율이 낮아지고 일반화를 통해 모델을 신뢰할 수 있습니다.
우선 우리는 Forward Propagation 에서 오차율이 최소화되는 W 값을 찾는 과정을 Gradient Descent 라고 합니다.

짚고 넘어가는 사전 지식

참고 1 : 미분으로 function 의 변화량을 알 수 있다
참고 2 편미분이란?
하나 이상의 변수를 갖는 함수 f 가 주어졌다고 가정하자. 예를 들어,

이 함수의 그래프는 유클리드 공간 속 곡면을 정의한다. 곡면 속 점마다 무한히 많은 접선이 존재한다. 편미분은 이런 접선 가운데 하나를 골라, 그 기울기를 구하는 것이다.
점 (x, y) 에서 x z 평면과 평행하는 접선의 기울기를 구하자. y 를 상수로 볼 때, 곡면 위에 놓인 곡선을 얻는다.
그 곡선 방정식에서 y 를 상수로 보아 미분을 구하면, 점 (x, y)에서 곡선의 기울기가 다음과 같다는 것을 알 수 있다.

대입을 통해, 점 (x, y) 에서 x z 평면과 평행하는 접선의 기울기는 3이라는 것을 알 수 있다.
즉, 점 (1, 1)에서 z의 x 에 대한 편미분은 3이다.
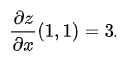

Chain rule

Question:
만약 f(x) = 2x 이고 g(x) = x^2 일때
F(g(x)) 의 미분값은 무엇일까?
Answer:
체인룰의 솔루션 : F(g(x)) 의 미분은 g(x)의 미분 곱하기 f(x)의 미분 값과 같다
f(x) = 2x의 미분값은 2
g(x) = x^2 의 미분값은 2x
따라서 F(g(x)) 의 미분값은 4x 이다.

Forward Propagation 에서는 Input 이 weight 백터와 이전 layer 의 output 이다.
따라서 Back Propagation 에서는 우리 error function 의 편미분값으로 네트워크 안의 각 개별 weight 업데이트시킬 수 있다.

에러의 백프로파게이션은 gradient descent 를 이용한 weight 의 개선을 하기 위해서 필요하다.
어떠한 weight 편미분은 네트워크 안의 에러의 기울기이고
우리는 체인룰을 에러의 gradient 인 편미분을 계산하기 위해
각 weight propagation 를 모든 네트워크 안의 가능한 path 에서 체인룰을 적용함으로써 이용할 수 있다.
심플하게 보는 Back Propagation 절차

이 딥러닝 네트워크의 백워드를 살펴보면, 현재 레이어의 에러는 현재 아웃풋의 미분값과 현재 히든레이어의 에러와 weight 합산곱을 곱해서 얻습니다.

Weight 의 미분은 아웃풋과 그 error 를 곱해서 얻을 수 있습니다.

인풋 W의 미분값의 합을 아래와 같다고 할 때

현재 W값들은 위의 값에 러닝레이트를 곱하여 업데이트할 수 있습니다.

이것을 반복하였을때 W 값들이 개선되는 것을 볼 수 있습니다.

참고 사이트
'AI시작' 카테고리의 다른 글
| 3-4. MNIST 분석 (0) | 2019.09.02 |
|---|---|
| 1. 딥러닝 영상분석 3총사를 구분하시나요 (0) | 2019.09.01 |
| 3-3 활성화 함수 (0) | 2019.08.19 |
| 내가 보려고 정리한 AI 용어와 개념 설명 (0) | 2019.08.19 |
| 잠시 KNN, k-최근접 이웃 알고리즘 (0) | 2019.08.19 |

